Motivation
Our study was motivated by a recent observation of the discoid cockroach (Blaberus discoidalis) self-righting from an upside-down orientation on a level, flat surface.

Fig. 1 Discoid cockroach’s strenuous, leg-assisted, winged ground self-righting.
One strategy of the animal is to push both its wings together against the ground to pitch over its head (Fig. 2, blue arrow). However, such a somersault has a large potential energy barrier. The animal is often trapped in a metastable state, where its center of mass projection falls within a triangular base of support formed by the head and outer edges of two wings in contact with the ground (Fig. 2, yellow arrows and triangle).
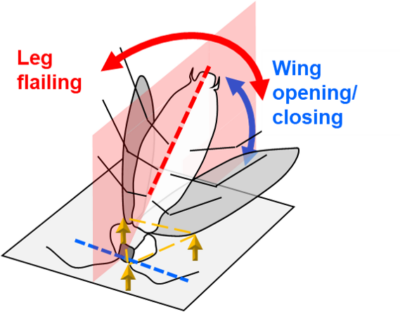
Fig. 2 Schematic of animal in a metastable state.
To overcome the barrier, the animal often flails its legs laterally (Fig. 2, red arrow) and flexes and twists its abdomen. These motions induce kinetic energy fluctuation to perturb the body to roll, which overcomes a smaller potential energy barrier. However, injected KE is dissipated via collision and friction against the ground and internal collision (wings and legs stop moving relative to the body). Thus, coordination between the wing and leg oscillations may be critical for self-righting.
Randomness observed in animals’ self-righting
Curiously, compared to cockroach walking and running, in strenuous, leg-assisted, winged self-righting, we observed that both wing and leg oscillations are much less periodic, with large randomness present in their amplitudes, directions, speeds, and periods. We hypothesize that the unusually large randomness in motions is beneficial for strenuous, leg-assisted, winged ground self-righting, by allowing random search in appendage configuration space to find an appropriate appendage coordination.
Simulation robot design
To test our hypothesis, we took an approach of robotic modeling and created a simplified computational model—a cockroach-inspired simulation robot—to perform systematic in silico experiments (Fig. 3).
Our simulation robot was created using Chrono, an open-source, high-fidelity, multi-body dynamics engine. The robot has two wings, a pendulum “leg”, and a body with a head that protrudes beyond the anterior end of the wings (mimicking the cockroach’s head. The two wings open and close symmetrically, and the single-leg swings side to side to generate lateral perturbation.
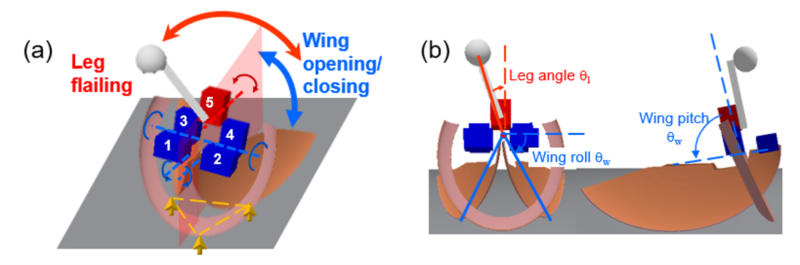
Fig. 3 Cockroach-inspired, leg-assisted, winged self-righting simulation robot.
Comparison between simulation and physical robot experiments
Qualitatively, the simulation robot displayed similar self-righting motion as the physical robot (Fig. 4).
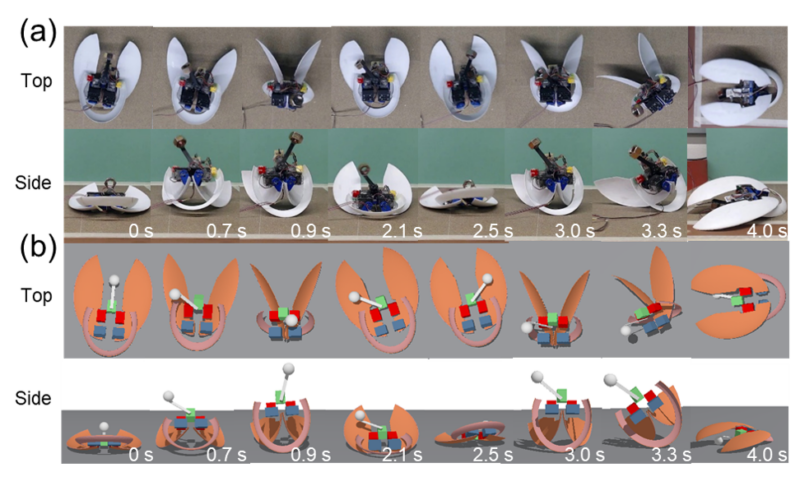
Fig. 4 Validation of simulation robot against a physical robot.
Randomness added in simulation
As a first step to understand the role of randomness in wing-leg coordination, we added Gaussian noise of variable levels to wing oscillation period (Fig. 5). We chose to only add noise to the time that wings are held closed, so that other parameters (wing opening/closing speed, wing opening amplitudes, wing opening time) were kept constant. We measured the level of randomness using coefficient of variation, Cv, defined as the ratio between standard deviation s and leg period Tl. In addition, we varied wing opening and leg flailing amplitudes to study the effect of randomness over a wide range of parameter space.
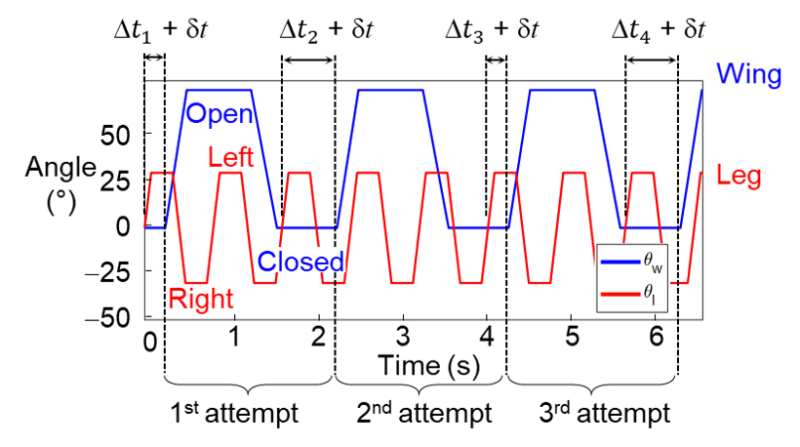
Fig. 5 Actuation profiles of wings (blue) and leg (red). ∆ti is the time delay of the ith wing opening attempt, defined as the time interval between wing opening moment and the start of the preceding leg oscillation. A Gaussian noise δt is added to ∆t in simulation experiments with randomness.
Randomness in coordination increases self-righting probability
Without randomness in wing-leg coordination, self-righting outcome of the robot was deterministic (Fig. 6, Cv = 0%). With randomness, self-righting outcome became stochastic (Fig. 6, Cv > 0%). When θw and θl were too small or too large, self-righting probability was nearly always zero or one, not strongly affected by randomness. However, at intermediate θw and θl near the boundary between success and failure without randomness (Cv = 0%), increasing level of randomness in wing-leg coordination significantly increased the robot’s self-righting probability (Fig. 6, Cv = 0-25%). These results suggested that, when a cockroach is too tired (weak wing pushing and/or leg flailing), randomness does not help; when it is very energetic (strong wing pushing and/or leg flailing), randomness does not matter. However, when an animal is nearly or barely able to self-right (intermediate wing pushing and leg flailing), which is frequent in strenuous self-righting, randomness in coordination significantly increases its chance of success.
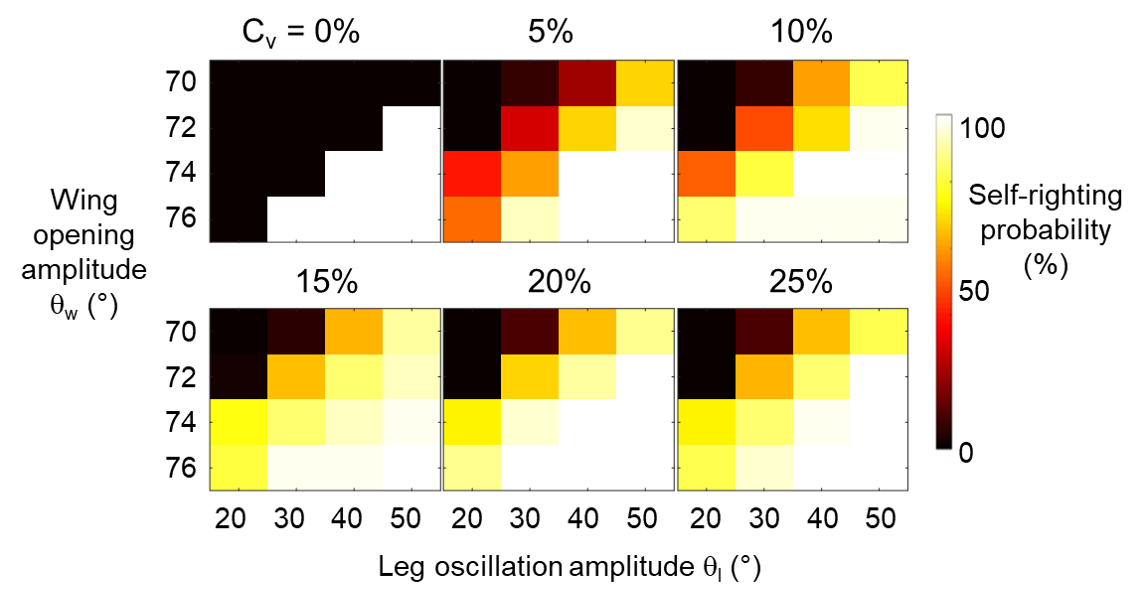
Fig, 6 Effect of randomness on self-righting probability within 10 s for each trial.
Randomness in coordination changes phase between wing and leg oscillations
Because we only added randomness to wing oscillation period while keeping everything else constant, the only thing that changed was the phase between wing and leg oscillations at each wing opening attempt (Fig. 5). For each wing opening attempt i, we defined the phase φ between wing and leg oscillations as the ratio of time delay ∆ti to leg period Tl. The initial phase was thus φ1 = ∆t1/ Tl. To study the effect of phase for a single wing opening attempt, we varied φ from 0% to 100% with an increment of 5% for each combination of qw and ql tested, without adding randomness.
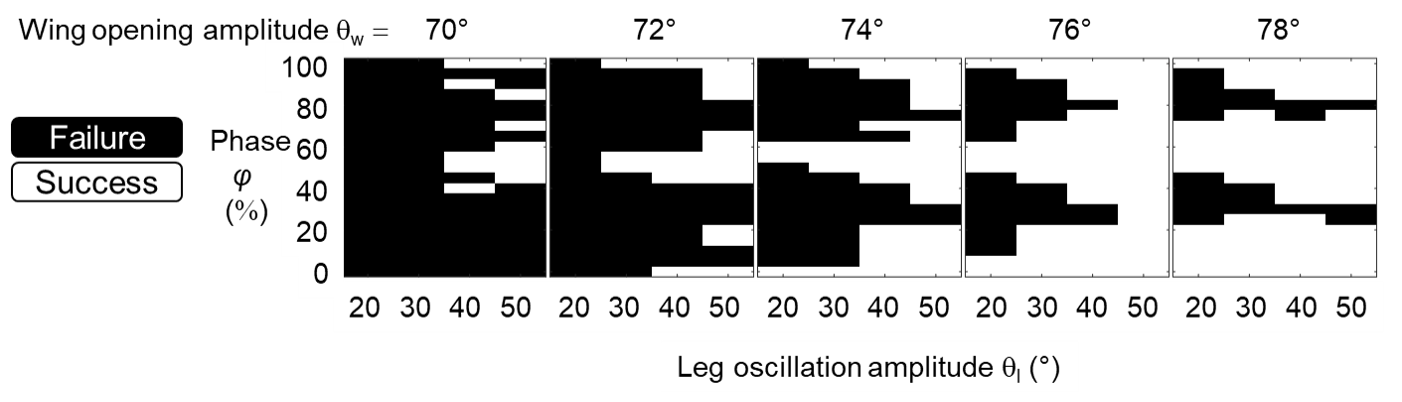
Fig. 7 Dependence of self-righting outcome of a single attempt on phase (single-attempt phase map).
From our results of self-righting outcome after a single attempt without randomness in coordination, we find the phase between wing and leg oscillations had a strong impact on self-righting outcome at intermediate wing opening and leg oscillation amplitudes. Empirically, some “good” phases led to success (e.g., phases around φ = 0%, 50%, and 100%), whereas other “bad” phases led to failure (e.g., phases around φ = 25% and 80%).
Randomness allows stochastic visits of good phases
Without randomness, wing and leg actuation were periodic. This resulted in a limited number of phases that could be visited during consecutive attempts. If the phases that could be visited happened to be bad for the wing and leg oscillation periods given, self-righting was never successful (Fig. 8(a, c)). With randomness added to the motion, the phase evolution was no longer periodic (Fig. 8(b, d)). Instead, the system could visit an infinite number of phases (any value from 0% to 100%) and was thus impossible to be trapped in bad phases, as long as there were good phases in the phase map.
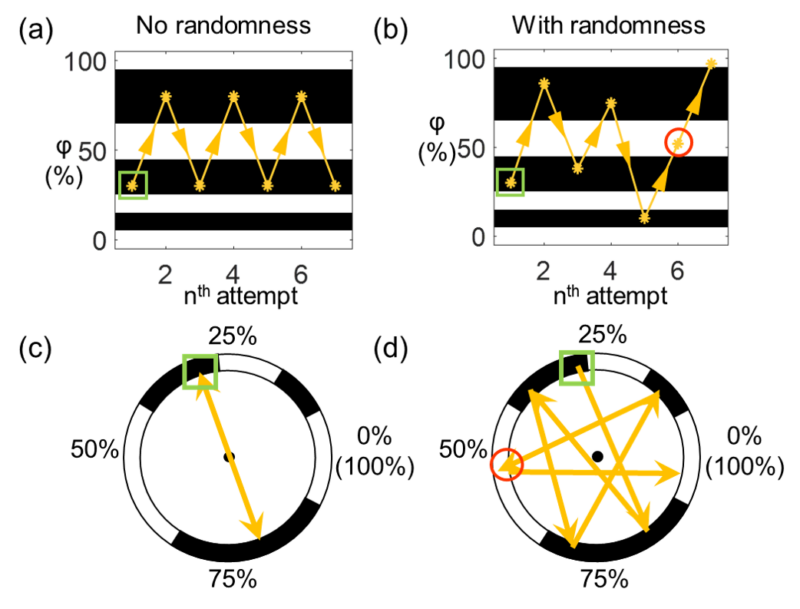
Fig. 8 Phase evolution over consecutive attempts (yellow points connected by arrows) on phase map (white: good phases, black: bad phases), without randomness (a, c) and with randomness (b, d).
Summary
We studied the impact of randomness in coordination between appendages during strenuous, leg-assisted, winged self-righting. We developed a simulation robot following the design and control of a recent physical robot to generate the strenuous self-righting behavior, and we used it to conduct systematic simulation experiments and analyses. We discovered that randomness in wing-leg coordination facilitated self-righting, especially at intermediate wing opening and leg oscillation amplitudes, when the system’s kinetic energy was about to overcome the potential energy barrier. Randomness allowed the system to explore various phases more thoroughly between wing and leg oscillations, thereby increasing the chance of finding a good coordination between them.
Related publications
