Motivation
To move effectively in nature, animals transition between different forms of movement (locomotor modes; eg., walk, run, climb, etc.). Robots are also required to similarly transition across diverse locomotor modes to traverse unavoidable obstacles during critical applications such as search and rescue in rubble, inspection and monitoring in buildings, extraterrestrial exploration through rocks, and even drug delivery inside a human body. However, robots still struggle to do so, because we do not understand well how locomotor transitions emerge from physical interaction with complex terrain.
To begin to understand how such transitions emerge from physical interaction with the terrain, we propose an energy landscape approach and demonstrate how it can reveal principles of locomotor transitions for a model system of cockroaches traversing beam-like obstacles.
Model system: Cockroaches traversing beam like obstacles
Our study is motivated by recent observations in a model system of insects traversing complex 3-D terrain. The discoid cockroach, native to rainforest floor, can traverse flexible, grass-like beam obstacles using many locomotor modes, stochastically transitioning across them via multiple pathways. For simplicity, hereafter we focus on the transition between two modes. The animal often first pushes against the beams, and beam elastic restoring forces lead the animal body to pitch up . After this, though, the animal rarely pushes across but often rolls to maneuver through beam gaps. We define these as “pitch” and “roll” modes.
Robotic physical model to enable systematic variation of parameters
To observe the physical interaction of body and beams, we developed and tested a minimalistic robotic physical model. The robot had an ellipsoid-like body that was propelled forward and was free to pitch and roll in response to interaction with the two beams.
Energy landscape modelling
Using the measured properties of the body and beams, we calculated the system potential energy (sum of body and beam gravitational energy and beam elastic energy) as a function of body pitch, roll, and forward position relative to the beams. Before the body contacted the beams, pitching or rolling increased body gravitational energy (because body is bottom heavy). Thus, the potential energy landscape over body pitch–roll space had a global minimum at zero pitch and zero roll, i.e., when the body was horizontal. As the body moved closer and interacted with the beams, the global minimum evolved into a “pitch” local minimum. Meanwhile, two “roll” local minima emerged, whose energies were lower than the pitch local minimum.
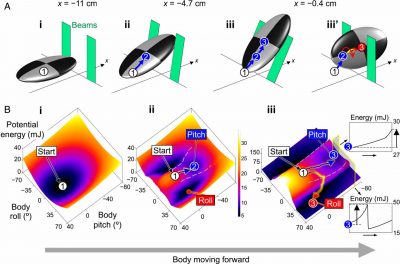
Robot locomotor transitions on a potential energy landscape. (A) Snapshots of body before and during interaction with two beams in pitch (i, ii, iii) and roll (iii’) modes. (B) Snapshots of landscape over body pitch-roll space before (i) and during (ii, iii) interaction. Representative system state trajectories are shown for being trapped in pitch basin (blue) and transitioning to roll basin (red). Insets in (iii) define potential energy barriers to escape from pitch local minimum in pitch-up and positive roll directions. Dashed gray curves on landscape show boundaries. between pitch and roll basins. Note that landscape evolves as body moves forward (increasing x), and only part of landscape over pitch-roll space is shown to focus on pitch and roll basins
System state is strongly attracted to an energy basin on landscape
We discovered that the system state during the observed pitch and roll modes were attracted to the pitch and roll basins, respectively. When the body was far away from the beams, the system state in pitch and roll space settled to the global minimum of the landscape. During beam interaction, without oscillation, the system state was trapped in the pitch basin, leading to the body pushing across the beams in a pitched-up orientation with little roll. With oscillation, the system escaped from the pitch basin and crossed a potential energy barrier to reach the roll basin, thereby transitioning from the pitch to the roll mode.
Kinetic energy fluctuation helps escape a landscape basin
We found that as the kinetic energy fluctuations from vertical oscillations increased, he system was more likely to escape from the pitch basin it was initially attracted to and reach the roll basin, resulting in more likely pitch-to-roll transitions.
Barrier to escape from pitch basin varied as body moved forward
The barrier to escape from pitch basin depended on both towards which direction the system moved in the pitch-roll space and body forward position relative to the beams. At each beam stiffness, when the body was not in contact with the beams, the escape barrier was large along all directions in the pitch-roll space. As the body moved forward, the escape barrier towards the direction of roll basins reduced drastically, becoming comparable to or even smaller than average kinetic energy fluctuation at the saddle point. By contrast, escape barrier in the direction of pitching up or down was always greater than average kinetic energy fluctuation.
Minimal escape barrier occurred at the saddle point between the pitch and roll basins. Only within a small range of body forward position was average kinetic energy fluctuation sufficient for overcoming pitch-to-roll transition barrier. The observed transitions were very likely to happen within this range.
Robot escape from pitch basin is more likely towards direction of lower barrier
The system state trajectories on the landscape showed that escape was more aligned with the direction of the saddle point between pitch and roll basins, i.e., escape was more likely towards the direction of lower barrier.
Favorability for locomotor transitions
Robot obstacle traversal across different beam stiffness further suggested a concept of favorability for locomotor transitions. Pitch-to-roll transition is more likely as beam stiffness increases. Intuitively, when the beams were flimsy, the body pushed across (trapped in the pitch mode) as if nothing were there; when the beams were rigid, the body could not push across and must roll. Thus, the likelihood of pitch-to-roll transition is positively correlated with how favorable transitioning to the roll mode is relative to staying in the pitch mode.
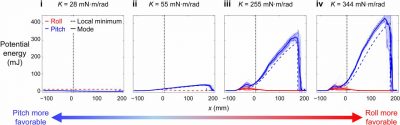
Favorability measure for robot. Potential energy of measured pitch and roll modes (solid) and of pitch and roll local minima (dashed) as a function of body forward position x. Measured data are for all f tested (n = 70 trials) at each beam stiffness K. Blue and red show trials trapped in pitch basin and transitioning to roll basin,respectively. Columns i-iv are at K = 28, 55, 255, and 344 mNm/rad.
To provide a measure of favorability, we compared whether the pitch or roll basin was lower in energy during traversal. At lowest beam stiffness, the pitch basin remained the global minimum basin throughout traversal indicating that the pitch mode was more favorable. As stiffness increased, the pitch basin became increasingly higher than the roll basin, indicating that the roll mode became increasingly more favorable. At the second beam stiffness (K = 55 mNm/rad), although the roll mode was more favorable as body moved forward, kinetic energy fluctuation was smaller than the transition barrier thus, transition did not occur. The negative correlation between the probability of staying in or transitioning to a mode and its relative basin height is only an emergent outcome of the transition physics.
Physical interaction with the terrain plays a major role in the animal’s locomotor transitions
Similar to the robot, animal’s system state during the pitch or roll mode was attracted to the corresponding basin of the energy landscape. Pitch-to-roll transition mostly occurred when both average kinetic energy fluctuation became comparable to transition barrier and the roll mode became more favorable (easier) than the pitch mode. Even when active behavior and sensing was likely at play during animal’s obstacle traversal, its locomotor transitions are also influenced by physical interaction with the terrain (captured by our energy landscape model).
Related publications
